L2E multivariate regression

L2E_multivariate performs multivariate regression under the L2 criterion. Available methods include proximal gradient descent (PG) and majorization-minimization (MM).

L2E_multivariate(
  y,
  X,
  beta,
  tau,
  method = "MM",
  max_iter = 100,
  tol = 1e-04,
  Show.Time = TRUE
)

Arguments

y	Response vector
X	Design matrix
beta	Initial vector of regression coefficients
tau	Initial precision estimate
method	Available methods include PG and MM. MM by default.
max_iter	Maximum number of iterations
tol	Relative tolerance
Show.Time	Report the computing time

Value

Returns a list object containing the estimates for beta (vector) and tau (scalar), the number of outer block descent iterations until convergence (scalar), and the number of inner iterations per outer iteration for updating beta (vector) and tau or eta (vector)

Examples

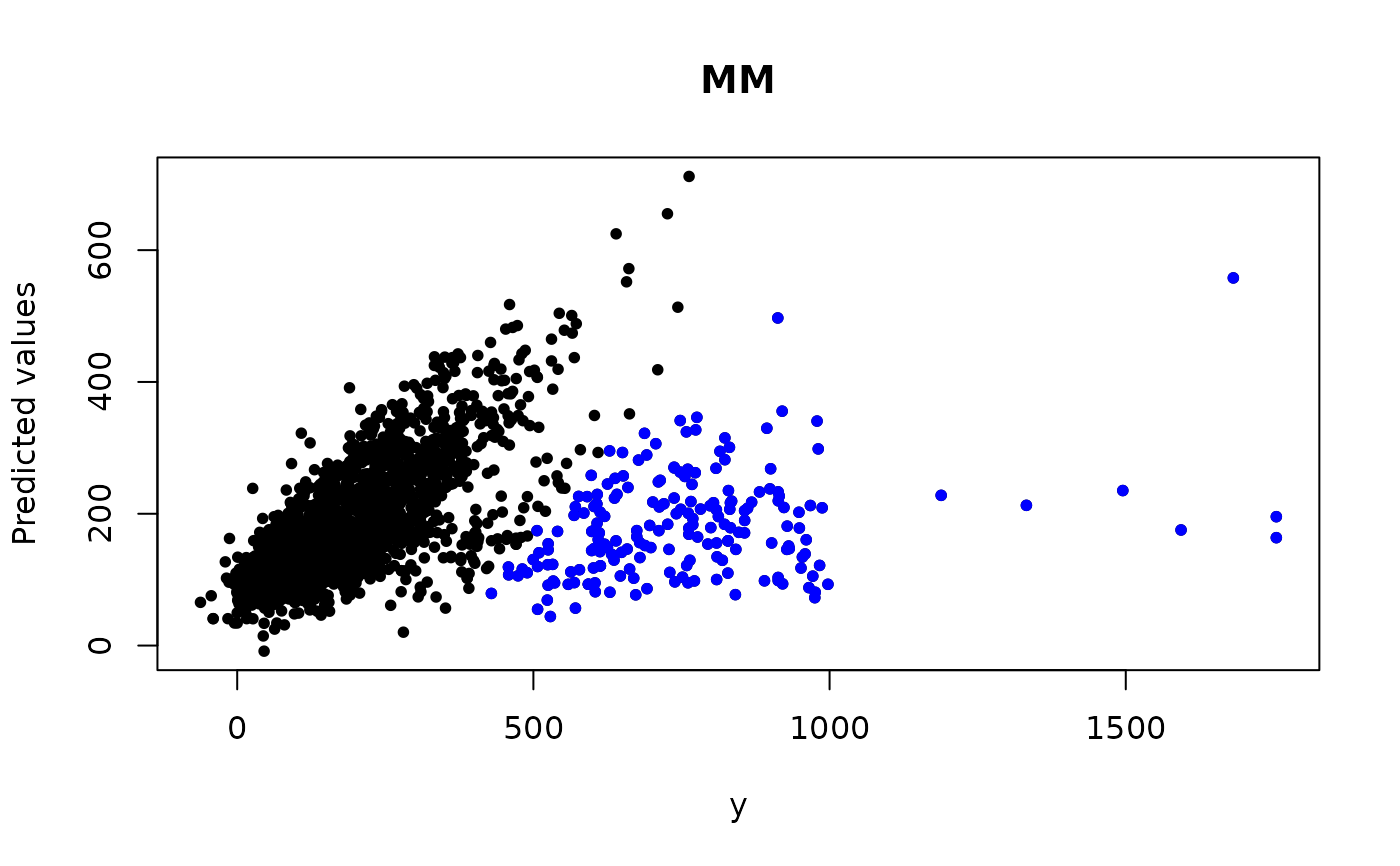
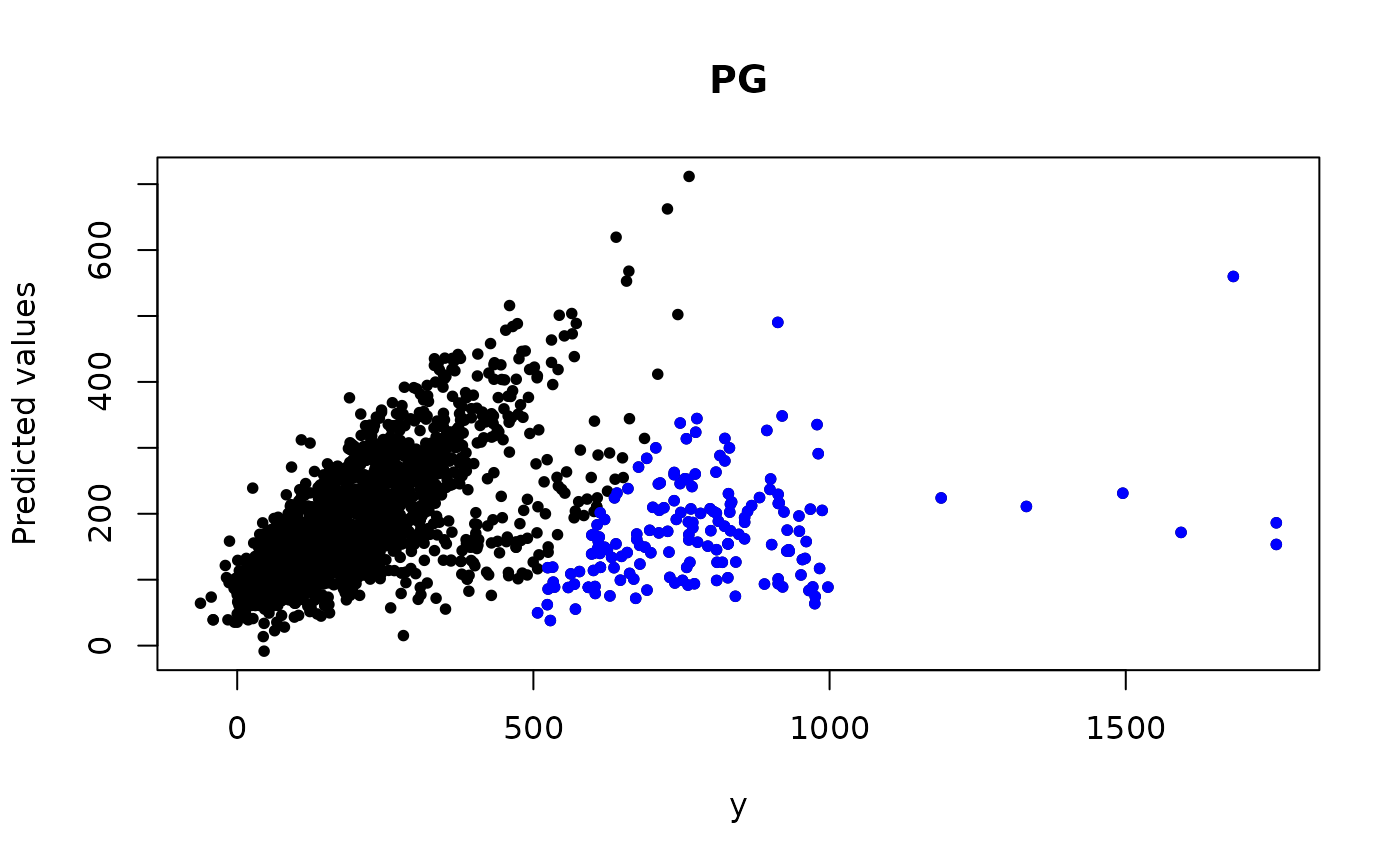
# Bank data example
y <- bank$y
X <- as.matrix(bank[,1:13])
X0 <- as.matrix(cbind(rep(1,length(y)), X))

tau <- 1/mad(y)
b <- matrix(0, 14, 1)

# MM method
sol_mm <- L2E_multivariate(y, X0, b, tau)
#>    user  system elapsed 
#>   0.073   0.000   0.073 
r_mm <- y - X0 %*% sol_mm$beta
ix_mm <- which(abs(r_mm) > 3/sol_mm$tau)
l2e_fit_mm <- X0 %*% sol_mm$beta

# PG method
sol_pg <- L2E_multivariate(y, X0, b, tau, method="PG")
#>    user  system elapsed 
#>   0.016   0.003   0.020 
r_pg <- y - X0 %*% sol_pg$beta
ix_pg <- which(abs(r_pg) > 3/sol_pg$tau)
l2e_fit_pg <- X0 %*% sol_pg$beta

plot(y, l2e_fit_mm, ylab='Predicted values', main='MM', pch=16, cex=0.8) # MM
points(y[ix_mm], l2e_fit_mm[ix_mm], pch=16, col='blue', cex=0.8) # MM
plot(y, l2e_fit_pg, ylab='Predicted values', main='PG', pch=16, cex=0.8) # PG
points(y[ix_pg], l2e_fit_pg[ix_pg], pch=16, col='blue', cex=0.8) # PG