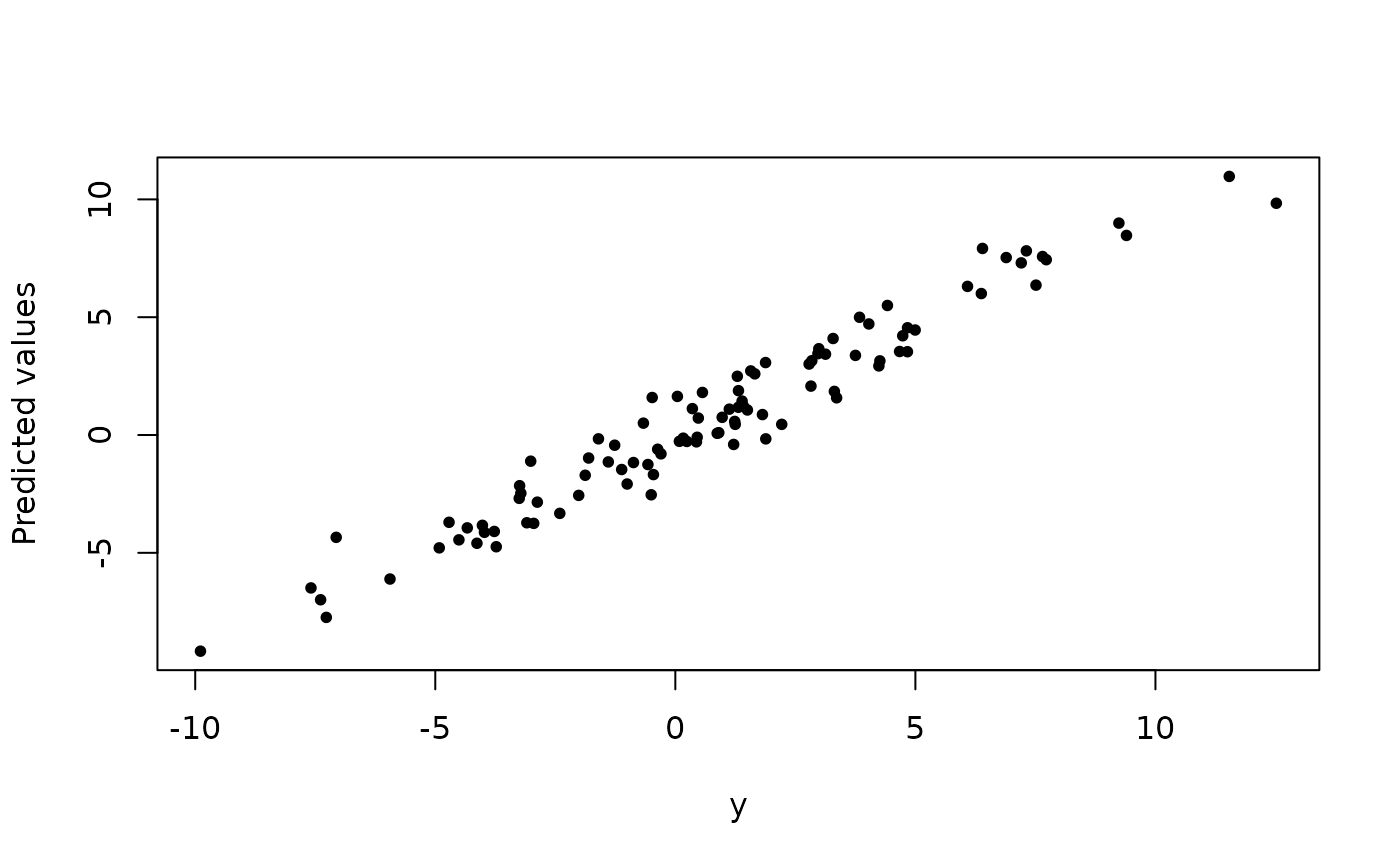
Solution path of L2E sparse regression with distance penalization

L2E_sparse_dist computes the solution path of the robust sparse regression under the L2 criterion with distance penalty

L2E_sparse_dist(
  y,
  X,
  beta0,
  tau0,
  kSeq,
  rhoSeq,
  stepsize = 0.9,
  sigma = 0.5,
  max_iter = 100,
  tol = 1e-04,
  Show.Time = TRUE
)

Arguments

y	Response vector
X	Design matrix
beta0	Initial vector of regression coefficients, can be omitted
tau0	Initial precision estimate, can be omitted
kSeq	A sequence of tuning parameter k, the number of nonzero entries in the estimated coefficients
rhoSeq	An increasing sequence of tuning parameter rho, can be omitted
stepsize	The stepsize parameter for the MM algorithm (0, 1)
sigma	The halving parameter sigma (0, 1)
max_iter	Maximum number of iterations
tol	Relative tolerance
Show.Time	Report the computing time

Value

Returns a list object containing the estimates for beta (matrix) and tau (vector) for each value of the tuning parameter k, the path of estimates for beta (list of matrices) and tau (matrix) for each value of rho, the run time (vector) for each k, and the sequence of rho and k used in the regression (vectors)

Examples

set.seed(12345)
n <- 100
tau <- 1
f <- matrix(c(rep(2,5), rep(0,45)), ncol = 1)
X <- X0 <- matrix(rnorm(n*50), nrow = n)
y <- y0 <- X0 %*% f + (1/tau)*rnorm(n)

## Clean Data
k <- 5
sol <- L2E_sparse_dist(y=y, X=X, kSeq=k)
#>    user  system elapsed 
#>   0.615   0.000   0.615 
r <- y - X %*% sol$Beta
ix <- which(abs(r) > 3/sol$Tau)
l2e_fit <- X %*% sol$Beta

plot(y, l2e_fit, ylab='Predicted values', pch=16, cex=0.8)
points(y[ix], l2e_fit[ix], pch=16, col='blue', cex=0.8)

## Contaminated Data
i <- 1:5
y[i] <- 2 + y0[i]
X[i,] <- 2 + X0[i,]

sol <- L2E_sparse_dist(y=y, X=X, kSeq=k)
#>    user  system elapsed 
#>   0.479   0.000   0.479 
r <- y - X %*% sol$Beta
ix <- which(abs(r) > 3/sol$Tau)
l2e_fit <- X %*% sol$Beta

plot(y, l2e_fit, ylab='Predicted values', pch=16, cex=0.8)
points(y[ix], l2e_fit[ix], pch=16, col='blue', cex=0.8)